Hilarious example of a problem which is so much harder than the tester thinks it is (and thus gets it wrong and says chatgpt is wrong for the wrong reasons on the first attempt). Oh and the ‘correct’ answer wrong, it’s an ok approximation but analytically incorrect. But the tester doesn’t even realize this because they are unqualified to run this test.
Oh and nobody in the comments appears to realize this either. And this show of math reasoning is ultimately a show of drawing a known and oft repeated basic arithmetic question for a math test that fails to interrogate the assumptions of the problem.
This is all hilariously infuriating, and I hope the two people who read the Lemmy comments enjoy the answer:
(Also also, the fact that chat gpt failed the easier version so many times is hilarious in its own right)
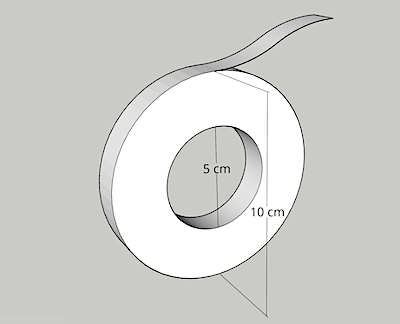
@ChatGPT@lemmings.world There is a roll of tape. The tape is 100 meters long when unrolled. When rolled up, the outer diameter is 10 cm, and the inner diameter is 5 cm. How thick is the tape?
To find the thickness of the tape, we need to consider the volume of the tape in both its rolled and unrolled forms.
First, let’s summarize the given information:
- The tape length when unrolled: ( L = 100 ) meters or ( 10000 ) cm.
- Outer diameter of the roll: ( D_\text{outer} = 10 ) cm, so the outer radius ( R_\text{outer} = 5 ) cm.
- Inner diameter of the roll: ( D_\text{inner} = 5 ) cm, so the inner radius ( R_\text{inner} = 2.5 ) cm.
Step 1: Calculate the Volume of the Tape
The volume ( V ) of the tape can be found by calculating the volume of the cylindrical shell formed by the tape: [ V = \pi \left( R_\text{outer}^2 - R_\text{inner}^2 \right) \times \text{Width of the tape} ]
Let ( t ) be the thickness of the tape, then:
[ V = \pi (R_\text{outer}^2 - R_\text{inner}^2) \cdot t ]
Step 2: Relation Between Volume and Length When Unrolled
When the tape is unrolled, its volume is:
[ V = \text{Length} \times \text{Width} \times \text{Thickness} ]
Given the length ( L = 10000 ) cm and the tape width ( t ), we have:
[ V = 10000 \times \text{Width} \times \text{Thickness} ]
Since the volume remains the same when rolled or unrolled, we equate the two expressions for volume:
[ \pi (R_\text{outer}^2 - R_\text{inner}^2) \cdot t = 10000 \cdot \text{Width} \cdot t ]
Step 3: Solve for the Thickness
Divide both sides by ( t ):
[ \pi (R_\text{outer}^2 - R_\text{inner}^2) = 10000 \cdot \text{Width} ]
Given that ( \text{Width} ) appears on both sides, it cancels out:
[ t = \frac{\pi (R_\text{outer}^2 - R_\text{inner}^2)}{10000} ]
Substitute ( R_\text{outer} = 5 ) cm and ( R_\text{inner} = 2.5 ) cm:
[ t = \frac{\pi (5^2 - 2.5^2)}{10000} ] [ t = \frac{\pi (25 - 6.25)}{10000} ] [ t = \frac{\pi \cdot 18.75}{10000} ] [ t = \frac{18.75\pi}{10000} ] [ t \approx \frac{58.9055}{10000} ] [ t \approx 0.00589 \text{ cm} ]
Therefore, the thickness of the tape is approximately ( 0.00589 ) cm, or ( 0.0589 ) mm.
If you have any questions or need further details, feel free to ask!
To find the thickness of the tape, we can use the given information about the total length of the tape, the outer diameter, and the inner diameter when the tape is rolled up.
First, we can calculate the cross-sectional area of the tape when it’s rolled up by considering it as a cylindrical shell. The formula for the area of a cylindrical shell is given by the difference of the areas of two circles (the outer circle and the inner circle).
-
Convert diameters to radii in meters:
[ \text{Outer radius ®} = \frac{10 , \text{cm}}{2} = 5 , \text{cm} = 0.05 , \text{m} ]
[ \text{Inner radius ®} = \frac{5 , \text{cm}}{2} = 2.5 , \text{cm} = 0.025 , \text{m} ]
-
Calculate the area of the cross section:
[ \text{Area of the cylindrical shell (A)} = \pi (R^2 - r^2) = \pi (0.05^2 - 0.025^2) ]
[ A = \pi (0.0025 - 0.000625) = \pi \times 0.001875 \approx 0.00589 , \text{square meters} ]
-
Determine the thickness of the tape (t):
Since the tape is 100 meters long and the cross-sectional area is (0.00589 , \text{m}^2), the volume (V) of the tape can be calculated using:
[ V = \text{length} \times \text{thickness} = A \times t ]
Solving for (t):
[ t = \frac{V}{A} = \frac{\text{length}}{A} = \frac{100 , \text{m}}{0.00589 , \text{m}^2} ]
[ t \approx 0.0016964 , \text{meters} ]
Converting this thickness into millimeters:
[ t \approx 0.0016964 , \text{m} \times 1000 = 1.6964 , \text{mm} ]
Therefore, the thickness of the tape is approximately 1.70 mm.
-